Aménagement paysager**

Dans une entreprise d'aménagement paysager, un jardinier est chargé de concevoir un parterre de fleurs rectangulaire le long d'un mur. Il dispose de 26 m de bordure pour entourer trois côtés du parterre (le quatrième côté est appuyé sur le mur du jardin).

Problématique : quelles doivent être les dimensions du parterre pour que l'aire du parterre soit maximale ? Quelle est l'aire maximale du parterre de fleurs ?

Coup de pouce : une perle est là pour vous aider !

On nomme `x` la longueur du côté perpendiculaire au mur, exprimée en mètres.

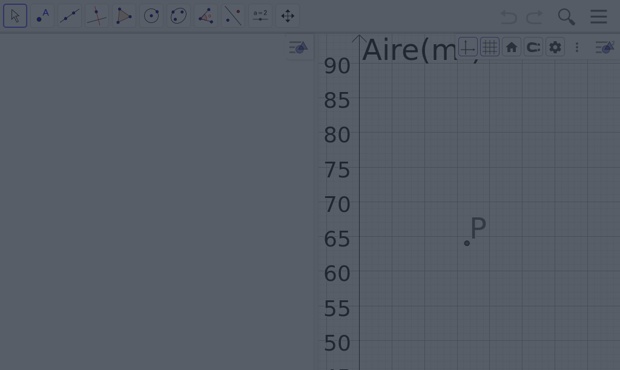
1. À l'aide de la simulation GeoGebra ci-dessous, déterminer l'aire du parterre de fleurs pour `x=2` puis `x=9`.

2. Exprimer la longueur `L(x)` du côté parallèle au mur en fonction de \(x\).

3. Montrer que l'aire `A(x)` du parterre de fleurs peut s'écrire \(A(x)=-2x(x-13)\).

4. Déterminer les racines du polynôme \(A(x)\).

5. Calculer l'abscisse \(x_{s}\) du sommet de la parabole.

6. Calculer l'aire maximum du parterre de fleurs.

7. Valider votre résultat à l'aide de la simulation.

8. Répondre à la problématique de l'activité.